A Hermitian Einstein-Weyl manifold is a complex manifold
admitting a Ricci-flat Kähler covering
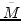
,
with the deck group acting on
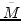
by
homotheties. If compact, it admits a canonical
Vaisman metric, due to Gauduchon.
We show that a Hermitian Einstein-Weyl structure
on a compact complex manifold is determined
by its volume form. This result is
a conformal analogue of Calabi's theorem
stating the uniqueness of Kähler metrics
with a given volume form in a given Kähler
class. We prove that
the solution of the conformal version of complex
Monge-Ampère equation is unique.
We conjecture that a Hermitian Einstein-Weyl
structure on a compact complex manifold
is unique, up to a holomorphic automorphism,
and compare this conjecture to Bando-Mabuchi
theorem.