Next: Mircea Sofonea: Tykhonov triples Up: TOME 65 (113), no. 1, 2022 Previous: Nimra Javed, Gerhard Pfister:
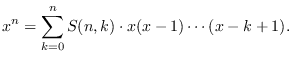
We also present a combinatorial proof (based on Feller's coupling) of the defining identity for the Stirling numbers of the first kind in the group of signed permutations.
Our proofs are self-contained and accessible also for non-experts.
Key Words: Stirling number, signed partitions, 'balls into urns' approach.
2010 Mathematics Subject Classification: Primary 05A18; Secondary 05A19.