Let
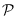
be a family of paths in a connected graph
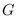
so that
there exists a
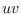
-path in
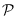
for every choice of vertices
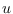
and
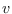
.
The
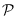
-interval
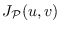
is the union of vertex sets of all
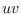
-paths in
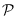
.
We address the problem of maximizing
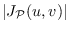
over all vertices
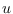
and
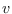
, for various families
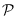
of paths.
- First, the Boolean distance between two vertices
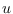 and
and 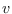 , in a connected graph
, in a connected graph 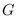 , equals the total number of vertices on
, equals the total number of vertices on 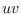 -paths.
The Boolean diameter of a connected graph is its maximum Boolean distance.
We observe that the Boolean diameter of any graph
-paths.
The Boolean diameter of a connected graph is its maximum Boolean distance.
We observe that the Boolean diameter of any graph 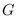 can be computed in linear time, due to an elegant characterization of Boolean distances by [Harary, Melter, Peled & Tomescu; Discr. Math. 1982].
can be computed in linear time, due to an elegant characterization of Boolean distances by [Harary, Melter, Peled & Tomescu; Discr. Math. 1982].
- Then, we restrict our study to induced paths. Unless P=NP, we cannot compute in polynomial time the maximum number of vertices on all induced paths between two vertices. However, on the positive side, we can solve this problem in polynomial time on graphs of bounded clique-width, and even in linear time on bounded-treewidth graphs and distance-hereditary graphs.
- Finally, we introduce the interval semidistance for graphs, that only accounts for vertices on shortest paths. Equivalently, the interval semidistance between two vertices
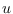 and
and 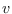 , in a connected graph
, in a connected graph 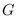 , equals the number of vertices that are metrically between
, equals the number of vertices that are metrically between 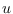 and
and 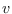 . The interval diameter (maximum interval semidistance) can be computed in
. The interval diameter (maximum interval semidistance) can be computed in
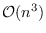 time for
time for 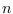 -vertex connected graphs. We prove that in contrast to Boolean diameter there is an
-vertex connected graphs. We prove that in contrast to Boolean diameter there is an
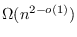 time lower bound for this problem under the Strong Exponential-Time Hypothesis, even for graphs with only
time lower bound for this problem under the Strong Exponential-Time Hypothesis, even for graphs with only
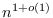 edges. However, on the positive side, we present linear-time algorithms for computing the interval diameter within various graph classes with tree-likeness properties, such as: trees, cacti, block graphs and distance-hereditary graphs.
edges. However, on the positive side, we present linear-time algorithms for computing the interval diameter within various graph classes with tree-likeness properties, such as: trees, cacti, block graphs and distance-hereditary graphs.