La mesure de Mahler est multiplicative: pour tout polynôme
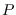
et
tout entier positif
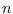
, on a
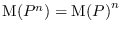
. La hauteur d'un polynôme ne
possède pas cette propriété et le problème de la relation
entre la hauteur d'un polynôme et de ses puissances se pose. John
Abbott, en recherchant les polynômes dont les hauteurs des carrés sont plus petites que celle du polynôme initial, a conjecturé que la hauteur du carré d'un polynôme est au moins égale
au double de celle du polynôme initial, c'est la
conjecture
initiale d'Abbott. Il a ajouté une généralisation de cette
conjecture dans le cas des puissances quelconques. Le présent
travail est consacré à l'étude de ces conjectures et leur
démonstration dans certains cas.