A graph
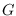
is called edge-magic if there exists a bijective function
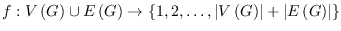
such that
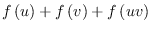
is a constant (called the valence of
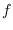
) for each
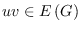
.
If
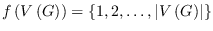
, then
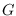
is called a super
edge-magic graph. A stronger version of edge-magic and super
edge-magic graphs appeared when the concepts of perfect edge-magic
and perfect super edge-magic graphs were introduced. The super
edge-magic deficiency
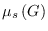
of a graph
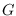
is
defined to be either the smallest nonnegative integer
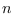
with the
property that
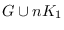
is super edge-magic or
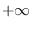
if
there exists no such integer
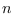
. On the other hand, the edge-magic
deficiency
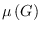
of a graph
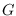
is the smallest
nonnegative integer
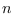
for which
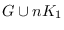
is edge-magic,
being
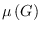
always finite. In this paper, the
concepts of (super) edge-magic deficiency are generalized using the
concepts of perfect (super) edge-magic graphs. This naturally leads
to the study of the valences of edge-magic and super edge-magic
labelings. We present some general results in this direction and
study the perfect (super) edge-magic deficiency of the star
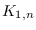
.