This note contains the following results for a ring A: (1) A is von Neumann regular if, and only if, every divisible singular
left A-module is p-injective and every p-injective left A-module is flat if and only if every simple right A-module and every
divisible singular left A-module are flat; (2) If A is a left YJ-injective ring whose simple left modules are either YJ-injective
or projective and g:
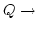
M is an epimorphism of left A-modules Q, M, where

Q is CE-injective, then Z(M), the singular submodule of M,
is a direct summand of M; (3) A is semi-simple, Artinian if and only if every semi-simple left A-module is quasi-injective and p-injective;
(4) If every maximal left ideal of A is either injective or a two-sided ideal of A and every simple left A-module is YJ-injective,
then A is either strongly regular or left self-injective regular with non-zero socle; (5) A right Noetherian, fully left idempotent ring
is biregular; (6) A is strongly regular if and only if A is a reduced left p.p. ring having a classical left quotient ring such that for
every proper principal left ideal P of A, r(P)

0; (7) A ring whose p-injective modules are injective and flat must be quasi-Frobenius;
(8) If every essential left ideal of A is an idempotent two-sided ideal of A, then the centre of A is von Neumann regular.