Sizhong Zhou: Degree conditions and path factors with inclusion or exclusion properties, 3-14

Abstract:

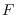
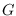
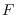
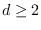
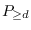
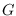
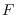
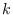
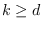
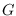
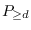
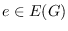
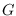
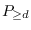
A spanning subgraph $F$ of a graph $G$ is called a path factor if every component of $F$ is a path. For an integer $d\geq2$, a $P_{\geq d}$-factor of a graph $G$ is a spanning subgraph $F$ such that every component is isomorphic to a path of $k$ vertices for some $k\geq d$. A graph $G$ is called a $P_{\geq d}$-factor covered graph if for any $e\in E(G)$, $G$ has a $P_{\geq d}$-factor covering $e$. 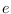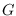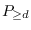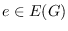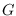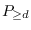A graph $G$ is called a $P_{\geq d}$-factor deleted graph if for any $e\in E(G)$, $G$ has a $P_{\geq d}$-factor excluding $e$. 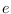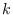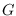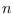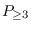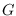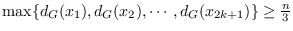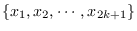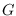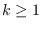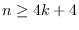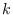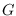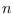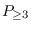In this article, we verify that (i) a $k$-connected graph $G$ with at least $n$ vertices admits a $P_{\geq3}$-factor if $G$ satisfies $\max\{d_G(x_1),d_G(x_2),\cdots,d_G(x_{2k+1})\}\geq\frac{n}{3}$ for any independent subset $\{x_1,x_2,\cdots,x_{2k+1}\}$ of $G$, where $k\geq1$ and $n\geq4k+4$ are two integers; (ii) a $k$-connected graph $G$ with at least $n$ vertices is a $P_{\geq3}$-factor covered graph if $G$ 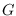satisfies $\max\{d_G(x_1),d_G(x_2),\cdots,d_G(x_{2k-1})\}\geq\frac{n+2}{3}$ 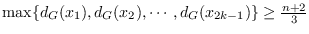for any independent subset $\{x_1,x_2,\cdots,x_{2k-1}\}$ 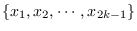of $G$, 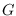where $k\geq1$ 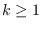and $n\geq4k+2$ 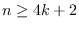are two integers; (iii) a $(k+1)$-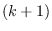connected graph $G$ 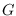with at least $n$ 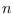vertices is a $P_{\geq3}$-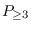factor deleted graph if $G$ 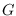satisfies $\max\{d_G(x_1),d_G(x_2),\cdots,d_G(x_{2k-1})\}\geq\frac{n}{3}$ 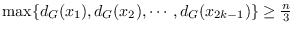for any independent subset $\{x_1,x_2,\cdots,x_{2k-1}\}$ 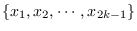of $G$, 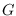where $k\geq1$ 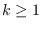and $n\geq4k+2$ 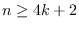are two integers.

Key Words: Graph, degree condition, $P_{\geq3}$-factor, $P_{\geq3}$-factor covered graph, $P_{\geq3}$-factor deleted graph.

2010 Mathematics Subject Classification: Primary 05C70; Secondary 05C38, 90B10.

Download the paper in pdf format here.