Jinyun Qi, Zhefeng Xu: The distribution of powers modulo $q$, 387-408

Abstract:

Let $\delta,\delta_{1}, \delta_{2}$ be any real numbers with $0<\delta,\delta_{1}, \delta_{2}\le 1$, and $q\ge 2$ be an integer, $h,k,l>1$ be any fixed non-zero pairwise distinct integers. In the present paper we use some estimates of exponential sums to study the distribution of integer powers modulo $q$. Define

$$N_{h,k,l,\delta_{1},\delta_{2}}(q) = \char93 \bigg\{a:0 < a \le ... ... \mathcal{A}_{h,k,\delta_{1}}(q) \cap \mathcal{A}_{k,l,\delta_{2}}(q) \bigg\},$$

where

$$\mathcal{A}_{h,k,\delta}(q) = \bigg\{a:0 < a\le q,(a,q)=1, \bigg\... ...ac{a^{h}}{q} \Big\} - \Big\{\frac{a^{k}}{q}\Big\} \bigg\vert < \delta \bigg\}.$$

We derive asymptotic formulas for $N_{h,k,l,\delta_{1},\delta_{2}}(q)$.

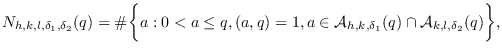
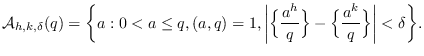
Key Words: Integer and its inverse, integer powers, exponential sums.

2020 Mathematics Subject Classification: Primary 11L03; Secondary 11N69.

Download the paper in pdf format here.