Ji-Cai Liu, Yuan-Yuan Zhao: Combinatorial proofs of two $q$-binomial coefficient identities, 381-386

Abstract:

We present combinatorial proofs of two $q$-binomial coefficient identities, which give two new $q$-analogues of the binomial coefficient identity:

$$\sum_{k=-\lfloor n/2\rfloor}^{\lfloor n/2\rfloor}(-1)^k{2n\choose n+2k}=2^n,$$

where $\lfloor x \rfloor$ denotes the integral part of real $x$.

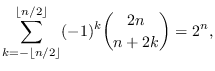Key Words: $q$-binomial coefficient, $q$-binomial theorem, combinatorial proof.

2020 Mathematics Subject Classification: Primary 05A19; Secondary 05A10.

Download the paper in pdf format here.