Xiao Wang, Jiankang Wang, Zhefeng Xu: Mean value of Ramanujan sum and Cochrane sums, 355-373

Abstract:

The main purpose of this paper is to study the mean value of Ramanujan sum $R_q(a)$ and generalized Cochrane sum $C(h,q,m,n)$ over incomplete intervals. Let ${\sum}'_{a}$ denote the summation over all $a$ such that $(a,q) = 1$, $k,l,s$ be positive integers and $\lambda_1,\lambda_2$ be real numbers with $0<\lambda_1, \lambda_2\leq1$. Define

$$W_{q}(a,h,k,m,n)=\mathop{{\sum}'}_{a=1}^{q}C(ah,q,m,n)R^k_{q}(a+1).$$

Some interesting mean value formulas for

$$\mathop{{\sum}'}_{b\leq\lambda_1 q}\mathop{{\sum}'}_{d\leq\lambda_2 q}b^ld^sW_{q}(a,bd,k,m,n)$$

will be given by using mean value of Dirichlet L-function.

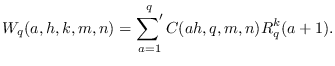
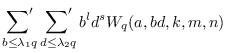
Key Words: Dirichlet L-function, Ramanujan sum, Cochrane sums, mean value.

2020 Mathematics Subject Classification: Primary 11M20; Secondary 11L05, 11F20.

Download the paper in pdf format here.