Evelia R. García Barroso, Arkadiusz Płoski: A note on the plane curve singularities in positive characteristic, 375-386

Abstract:

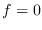
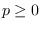
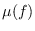
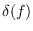
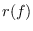
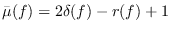
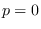
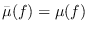
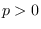
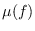
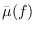
Given an algebroid plane curve $f=0$ over an algebraically closed field of characteristic $p\geq 0$ we consider the Milnor number $\mu(f)$, the delta invariant $\delta(f)$ and the number $r(f)$ of its irreducible components. Put $\bar \mu(f)=2\delta(f)-r(f)+1$. If $p=0$ then $\bar \mu (f)=\mu(f)$ (the Milnor formula). If $p>0$ $\mu(f)$ is not an invariant and $\bar \mu(f)$ plays the role of $\mu(f)$. 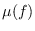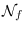Let $\mathcal N_f$ be the Newton polygon of $f$. 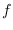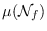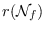We define the numbers $\mu(\mathcal N_{f})$ and $r(\mathcal N_{f})$ which can be computed by explicit formulas. 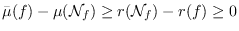The aim of this note is to give a simple proof of the inequality $\bar \mu(f)-\mu(\mathcal N_{f})\geq r(\mathcal N_{f})- r(f)\geq 0$ due to Boubakri, Greuel and Markwig. 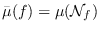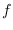We also prove that $\bar \mu(f)=\mu(\mathcal N_{f})$ when $f$ is non-degenerate.

Key Words: Milnor number, Newton polygon, non-degeneracy.

2020 Mathematics Subject Classification: Primary 14H20; Secondary 32S05.

Download the paper in pdf format here.