Abeer M. Albalahi, Igor Z. Milovanovic, Zahid Raza, Akbar Ali, Amjad E. Hamza: On the vertex-degree-function indices of connected $(n,m)$-graphs of maximum degree at most four, 3-13

Abstract:

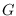
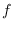
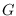
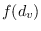
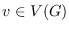
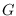
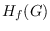
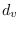
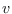
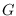
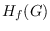
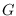
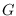
Consider a graph $G$ and a real-valued function $f$ defined on the degree set of $G$. The sum of the outputs $f(d_v)$ over all vertices $v\in V(G)$ of $G$ is usually known as the vertex-degree-function index and is denoted by $H_f(G)$, where $d_v$ represents the degree of a vertex $v$ of $G$. This paper gives sharp bounds on the index $H_f(G)$ in terms of order and size of $G$ when $G$ is connected and has the maximum degree at most $4$. 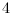All the graphs achieving the derived bounds are also determined. Bounds involving several existing indices - including the general zeroth-order Randic index and coindex, the general multiplicative first/second Zagreb index, the variable sum lodeg index, the variable sum exdeg index - are deduced as the special cases of the obtained ones.

Key Words: Chemical graph theory, topological index, vertex-degree-function indices, degree of a vertex.

2020 Mathematics Subject Classification: Primary 05C07, 05C09; Secondary 05C92.

Download the paper in pdf format here.